In this worksheet, you will…

Derive and review the General Multiplication Rule.
Develop methods to compute probabilities when events are dependent.
Practice identifying whether events are independent or dependent.

A quick notation note: in this lesson, I will often abbreviate $P(A\cap B)= P(A \text{ and } B)$ as $P(AB)$, as is often the case in probability textbooks.

Independence, Revisited

In the previous lesson (Probability Fundamentals), we discussed how to find $P(A\text{ and }B)$ when the events $A$ and $B$ are independent— knowing whether one event occurs has no bearing on whether the other is more or less likely to occur. In the case of independence, we simply multiply the probabilities:

If two events $A$ and $B$ are independent, then $P(AB) = P(A)P(B)$.

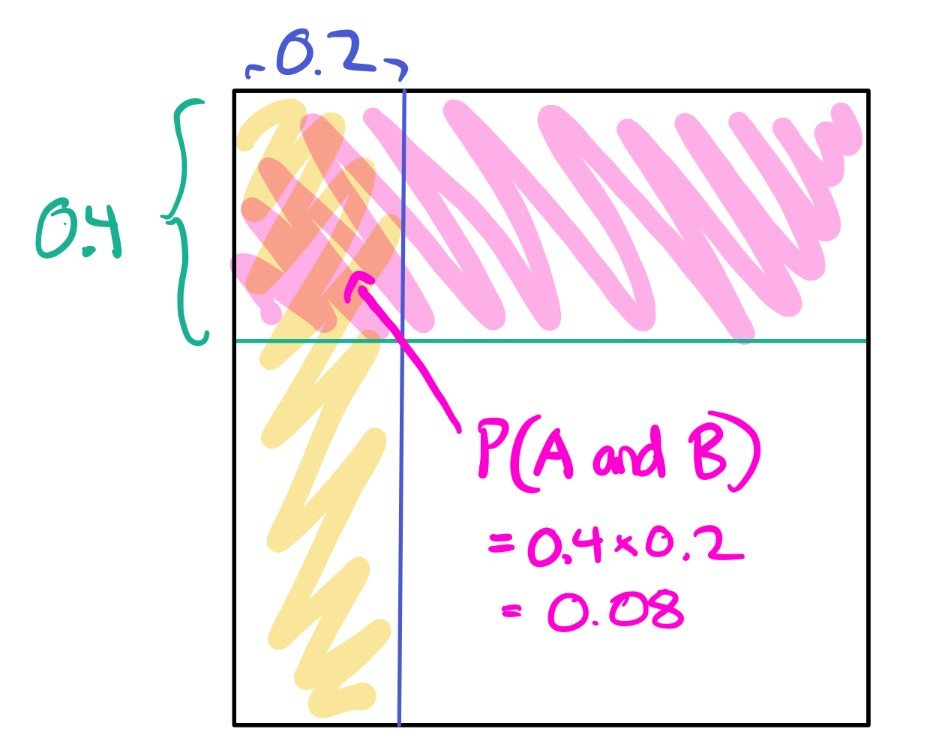
Here’s a way to visualize this: in each of the drawings below, we are visualizing each probability as an area that’s a subset of a square with total area equal to 1. To find the probability that both $A$ and $B$ occur, we look at the area of the overlapping region:

This diagram demonstrates (for this situation) that $P(AB) = P(A)P(B)$. However, why are $A$ and $B$ independent in this diagram? Consider picking a point at random on the square. $A$ happens if the point you pick is in the yellow rectangle on the left, and $B$ happens if it is in the pink rectangle at the top. Observe that whether $A$ occurs is determined entirely by the the horizontal location of the point, whereas $B$ is determined exclusively by the vertical location. So, if you know that $A$ happened (or didn’t happen), all that you learn is where your point might be horizontally— whether or not your point is left or right of the blue line that separates $A$ from the rest of $\Omega$. You gain no information about the vertical placement of the point. Thus, you have learned absolutely no information on whether $B$ may or may not have happened!

It turns out that this shortcut for independence is an if and only if condition, and more formally, the definition of independence:

Two events $A$ and $B$ are independent if and only if $P(A\cap B) = P(A)\cdot P(B)$.

However, independence is a very strict condition that often isn’t met. Consider these alternate ways that $A$ and $B$ could overlap, such that the area of the overlap is not simply a product of the areas:

In each of these cases, knowing whether $B$ occurs (i.e., whether your random point is in the pink circle) gives a whole lot of information about $A$. For the first case, knowing $B$ occurs makes $A$ seem a lot more likely— if your point was in $B$, it was most likely in the yellow region of the overlap between $A$ and $B$. In the second case, $B$ occurring makes $A$ a lot less likely. In the third case, knowing that $B$ occurs guarantees that $A$ occurred as well!

Similarly, for the first case, $P(AB)$ should be larger than multiplying $P(A)\cdot P(B)$. In the second, $P(AB)$ should be much smaller. In the last case, $P(AB)$ simply equals $P(B)$! As we can see, we need a new formula for what to do when these events are not independent.

The General Multiplication Rule

When events aren’t necessarily independent, we use the General Multiplication Rule for Probability:

For any two events $A$ and $B$, not necessarily independent, $P(A\cap B) = P(A) \cdot P(B | A)$.

The final term, $P(B | A)$, is read as “the probability of B, given A”. This is referred to as the conditional probability of an event $B$ given $A$. ($P(B)$ on its own is called the “unconditional” or “marginal” probability of $B$.) Because $A\cap B = B\cap A$, it would also be perfectly legitimate to write the General Multiplication Rule the other way around:

$$P(AB) = P(BA) = P(B) \cdot P(A | B)$$

This formula is only useful to determine $P(AB)$ when you have a way to determine $P(B |A)$ (or conversely, $P(A|B)$). For now, there are two methods for doing so:

$P(B|A)$ may be given (more or less) directly in the problem;
You must obtain $P(B|A)$ by determining how knowing that the event $A$ occurs changes the probability of $B$ occurring.

Let’s see these two methods in action.

Example 1: Factory defects

Suppose that two different factories produce a medical device. Factory A is larger and has better quality assurance, producing 80% of these devices with only 2% of the devices being defective. Factory B produces the remaining 20%, but has 6% defect rate due to being a newer factory. You receive a device in the mail, and you can’t tell which factory it came from. What is the probability that your device:

Came from Factory A and is defective?
Is defective (regardless of which factory it came from)?

Solution:

Notice that the event {Device came from factory A} and the event {Device is defective} are dependent events, because each factory has a different error rate.
Let’s define some events to make the writing shorter: let $A$ be the event the device came from factory A, $B$ be the event the device is from factory B (so $A^c = B$ in this case). Let $D$ be the event the device is defective. Reading this problem carefully, we can obtain a few pieces of given information: $P(A) = 0.8, P(B) = 0.2$, and $P(D | A) = 0.02, P(D | B) = 0.06$. From here, we can use what we need to use the Multiplication Rule:
$$P(A \text{ and } D) = P(A) \cdot P(D|A) $$
$$= 0.8*0.02=0.016$$
To find the marginal (overall) probability that the device is defective, observe that there are two ways this could happen. We could receive a defective device from A, OR a defective device from B! Since these events are mutually exclusive (a device can’t come from both factories), we can add the probabilities as follows:
$$P(D) = P(A \text{ and } D, \text{ OR } B \text{ and } D)$$
$$= P(AD) + P(BD)$$
$$= P(A)P(D|A) + P(B)P(D|B)$$
$$= 0.8\cdot 0.02 + 0.2 \cdot 0.06 = 0.028$$

Gut check: does this value of 2.8% like a reasonable answer? If we found the overall defect rate was outside of the 2% or 6% from both factories, that would certainly give me pause. So by that metric, we’re good! Reflect for yourself: Does it seem reasonable that our answer is closer to 2% than it is to 6%?

Example 2: Decks of Cards

Helpful context: A standard deck of playing cards contains 52 cards. Each card has one of 4 possible suits (red suits are hearts and diamonds, black suits are clubs and spades), and one of 13 possible ranks (the numbers 2-10, Jack, Queen, King, or Ace). Each suit-rank combination is represented exactly once, giving $4\cdot 13=52$cards. E.g., there’s 4 aces: the ace of hearts, ace of diamonds, ace of spades, and ace of clubs. We almost always assume the deck is well-shuffled, meaning that each possible reordering is equally likely, and thus each card is equally likely to be in any particular position in the deck.

Two cards are drawn from the top of a well-shuffled standard deck. What is the probability that both cards are aces?

Solution: These events are not independent, so we must proceed using the General Multiplication Rule,

$$P(\text{Card 1 ace and card 2 ace}) =$$

$$P(\text{Card 1 ace}) \cdot P(\text{Card 2 ace | Card 1 ace}) $$

Since there are 52 possible cards, 4 of which are aces, $P(\text{Card 1 ace}) = \frac{4}{52}$. For the conditional probability of the 2nd card being an ace (given the 1st was an ace), we note that since the 1st card is accounted for, there are 51 cards left in the deck, 3 of which are aces. (We don’t need to know which ace the first card was.) Thus, we find the solution as follows:

$$P(\text{Card 1 ace}) \cdot P(\text{Card 2 ace | Card 1 ace} = \frac{4}{52} \cdot \frac{3}{51} \approx 0.0045$$

How did we know to treat these events as dependent? In this case, knowing that the first card is an ace makes it less likely that the second card should be an ace (since we’ve removed one of the 4 possible aces from the deck). In general, you should assume events are dependent unless you can come up with a clear reason why they are independent. If you’re not sure, you can usually check!

Checking whether events are independent

Using the General Multiplication Rule, we can now establish a broader method of ways to check whether two events are independent. Since $P(AB) = P(A)P(B|A) = P(B)P(A|B)$ for all events $A$ and $B$, but simplifies to $P(A)P(B)$ if and only if the events are independent, we can establish the following rule:

For events $A$ and $B$ (with $P(A), P(B) \neq 0$), the following are all equivalent statements:

$A$ and $B$ are independent events;
$P(AB) = P(A)P(B)$;
$P(A | B) = P(A)$;
$P(B | A) = P(B)$.

By equivalent statements, we mean that if one is true, all are true, and if one is false, then all are false.

A subtle note: why did we need $P(A), P(B) \neq 0$? This is because $P(B|A)$ becomes a nebulous, ill-defined concept if $P(A) = 0$. You can ignore this edge case most of the time: If you do find $P(A)=0$, pretty much any probabilities you need to compute become much simpler to think about. (E.g., if $P(A)=0$, then $P(AB)=0$ and $P(A\cup B)=0$.)

Practice Problems

	Headaches	No Headaches	Total
Drug taken	50	150	200
Drug NOT taken	250	750	1000
Total	300	900	1200

Pharmaceutical manufacturers are interested to see whether a particular drug causes headaches as an unintended side effect. To do this, they survey 1200 people who use their products, and ask whether they took the drug in the last 24 hours and whether they’ve had a headache in the last 24 hours. The results are listed above (displayed in a contingency table):
- (a) What percent of survey respondents experienced headaches? Took the drug in the last 24 hours? Took the drug and experienced headaches?
- (b) Based on this information, does it appear that taking the drug is independent of experiencing headaches?
- (c) What assumptions are being made in this problem?
Suppose that $P(AB) = 0.4$ and $P(A) = 0.6$. Using the Multiplication Rule, calculate $P(B | A)$. Is it possible to find $P(B)$ from the information provided in this problem?
Draw two cards without replacement from a standard, well-shuffled deck. What is the chance the second card is an ace? (As a hint, the answer is not $\frac{4}{51}$, which is a common mistake for students to make.)
Draw two cards without replacement from a standard deck. Find the probability of each of the following events:
- $A=$ The cards are both hearts;
- $B=$ The cards are the same suit (heart, diamond, spade, or club);
- $C=$ The cards are the same rank (2-10, J, K, Q, or A).
- Are the events $A$ and $B$ independent? Are $B$ and $C$ independent?
Two standard six-sided dice are rolled. What is the chance the results are different? (You could answer this using a 6x6 grid, or by using the Multiplication Rule).
Three dice are rolled. What is the chance that their results are all different?

Answers are available here.